Desafios na construção de classificadores robustos em conjuntos de dados desbalanceados

Em alguns casos específicos de modelagem preditiva, lidamos com um problema conhecido como “classes desbalanceadas”. Isso acontece quando queremos classificar determinado exemplo, seja em tarefas binárias ou de múltiplas classes, mas os dados de treinamento específicos não apresentam uma distribuição equilibrada dessas classes.

Vamos usar um exemplo para facilitar. Estou estudando alguns modelos de previsão de fraudes, especialmente fraudes conhecidas como “Card Not Present Transactions Fraud”. Basicamente, são transações que acontecem sem que o cartão esteja fisicamente presente, o que é muito comum em compras online e assinaturas, como de plataformas de streaming ou e-commerce.

Com a popularização das carteiras digitais e pagamentos por aproximação, usando celular ou smartwatch, essas fraudes se tornaram cada vez mais comuns. Eu, por exemplo, quase sempre saio sem a carteira e raramente uso cartão físico.

A tarefa de prever essas fraudes é extremamente complexa, mas também muito útil para os bancos, emissores de cartões de crédito e empresas de meios de pagamento. Além das fraudes ocasionarem a perda de bilhões de dólares todos os anos, a experiência do cliente com a empresa pode deixar de ser positiva, quando identifica uma transação que não realizou, precisa cancelar o cartão, solicitar uma nova via, solicitar reembolso, etc. Em outras palavras, uma baita dor de cabeça, o que geralmente afeta o relacionamento desse cliente com a empresa.

Além da sua importância, o fato de serem eventos muito raros torna essa tarefa muito desafiadora. A cada $100 transacionados, apenas 68 centavos são resultado de fraudes, ou seja, menos de 1%. Isso significa que em um conjunto de dados com 100.000 exemplos para o treinamento de um modelo de classificação, apenas 680 são fraudes.

O modelo, então, precisa aprender a identificar fraudes sobre um número muito menor de exemplos. Se não forem tomados os cuidados adequados, nosso modelo pode se especializar em prever transações verdadeiras, enquanto tem dificuldades ou não aprende a detectar as fraudes.

Esse desafio não é exclusivo de sistemas financeiros. Em outras tarefas, como previsão de CHURN, identificação de células cancerígenas e triagem de currículos, os profissionais de ciência de dados enfrentam os mesmos desafios.

Vale destacar que, em situações de desbalanceamento, problemas binários são significativamente mais simples de trabalhar do que os de múltiplas classes, sendo este texto direcionado, principalmente, aos casos binários.

O objetivo desse texto é apresentar algumas das principais técnicas para lidar com classes desbalanceadas em modelos de classificação. Para isso, vamos discutir algumas abordagens complementares:

Reamostragem

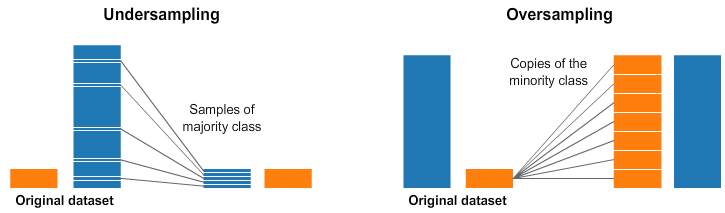
Existem duas técnicas principais de reamostragem, aplicadas antes da etapa de treinamento, que podem ajudar a tratar dados desbalanceados: undersampling e oversampling.

O undersampling consiste em remover exemplos aleatórios da classe majoritária, até atingir a distribuição desejada ou o equilíbrio entre as classes. Já o oversampling segue a mesma lógica, com a diferença que, nesse caso, são feitas cópias aleatórias dos exemplos da classe minoritária, até chegar à distribuição desejada.

Como você deve imaginar, ambas as técnicas possuem problemas graves, que precisam ser considerados durante seu uso. Ao deletar dados do seu conjunto de treino, você corre o risco de perder dados relevantes que podem prejudicar a generalização do modelo, causando underfitting.

O inverso também é verdade: ao duplicar muitos exemplos dos dados de treino, o risco é o modelo se adaptar muito aos casos específicos de treinamento, o que pode causar overfitting.

Ao usar técnicas de reamostragem é importante ressaltar que o modelo nunca deve ser testado nos dados transformados. A reamostragem é uma técnica usada durante o treino e a avaliação do modelo deve considerar os dados em sua distribuição original.

Outras técnicas mais avançadas foram pensadas para mitigar esses riscos de ajuste nos modelos, mas que seguem os mesmos princípios de provocar mudanças artificiais na distribuição original do conjunto de treinamento.

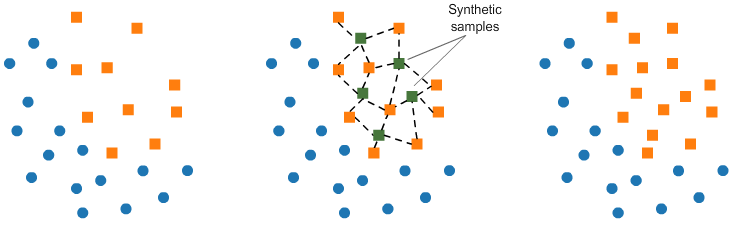
O SMOTE (Synthetic Minority Oversampling Technique) é um método alternativo de oversampling, que cria novos exemplos sintéticos da classe minoritária, através de combinações de exemplos existentes.

Esse método utiliza o algoritmo KNN para identificar e criar novas amostras que sigam a mesma tendência dos dados originais.

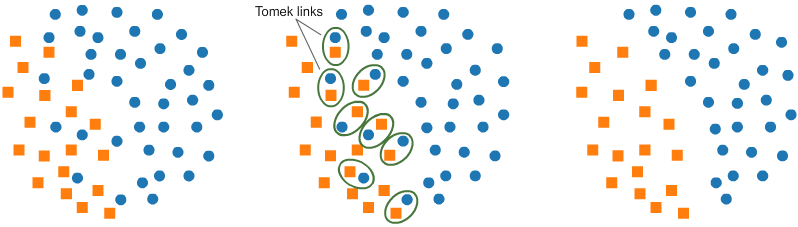
Outra técnica bastante utilizada é conhecida como Tomek Links. Ela identifica pares de exemplos de classes opostas que sejam muito próximos ou parecidos, em seguida, remove esses exemplos. Isso cria uma separação mais evidente dos dados, facilitando o processo de classificação.

Embora essa separação auxilie o modelo a aprender com mais eficácia, ela pode reduzir sua robustez, já que o modelo perde a capacidade de lidar adequadamente com exemplos próximos à fronteira de decisão.

Mas, afinal, como utilizar essas técnicas? Uma abordagem interessante é o Two-Phase Learning, ou aprendizado em duas etapas. Na primeira fase, um modelo inicial simples (weak learner) é treinado em um conjunto de dados reamostrado, utilizando técnicas como oversampling ou undersampling para corrigir o desbalanceamento. Esse modelo captura padrões gerais dos dados e suas previsões podem ser usadas como uma nova feature.

Na segunda fase, um modelo mais robusto é treinado nos dados originais, incorporando essa nova feature. Esse processo permite que o modelo robusto refine o aprendizado, capturando padrões mais sutis e ajustando-se melhor às classes minoritárias.

Essa abordagem não só melhora a capacidade do modelo em lidar com desbalanceamento, mas também reduz o risco de overfitting nos dados reamostrados ao usar o conjunto original na segunda fase.

Modelagem

As técnicas de modelagem consistem em métodos de nível algorítmico que não alteram a distribuição de dados original, mas tornam o modelo mais robusto para classes desbalanceadas.

Esse ajuste dos modelos poder ser feito através de mudanças na função de perda, que é essencialmente a forma que muitos modelos de machine learning aprendem. Nos modelos lineares, como Regressão Linear, a função de perda é usada para encontrar os coeficientes da reta que minimizam a soma dos erros quadrados.

Já em tarefas de classificação, a função de perda mais comum é chamada de Entropia Cruzada. Nessa função, o peso é o mesmo para todas as instâncias de treinamento, o que significa que predições incorretas são penalizadas independentemente da classe.

$$CE(y, \hat{y}) = - \frac{1}{N} \sum_{i=1}^{N} y_i \log(\hat{y}_i) + (1 - y_i) \log(1 - \hat{y}_i)$$

Para tornar o nosso modelo mais robusto para identificação de fraudes, podemos customizar a função de perda, fazendo com que ele preste mais atenção na predição das classes minoritárias. Essa abordagem é chamada de “aprendizado sensível ao custo” e existem algumas funções que podem nos ajudar a alcançar nosso objetivo. Vamos discutir duas delas: Class-Balanced Loss e Focal Loss.

A função de perda balanceada por classe (Class-Balanced Loss) torna o peso das predições inversamente proporcional ao número de amostras da classe no conjunto de treinamento. A ideia central é multiplicar o termo da perda original, geralmente Entropia Cruzada, por um peso inversamente proporcional à frequência da classe.

$$W_i = \frac{1}{(1 - \beta) N_i + \beta}$$ $$CB(y, \hat{y}) = \frac{1}{N} \sum_{i=1}^{N} W_i \cdot CE(y_i, \hat{y}_i)$$

Durante o treinamento, isso força o modelo a considerar com mais atenção as instâncias de classes menos representadas, corrigindo a tendência natural de favorecer a classe majoritária. Esse efeito reduz a influência do desbalanceamento no erro, melhorando a capacidade do modelo de classificar corretamente exemplos das classes menos representadas.

Já a função de perda focal (Focal Loss) tem como objetivo principal incentivar o modelo a focar no aprendizado dos exemplos mais difíceis, atribuindo um maior peso a essas predições. É uma variação da Entropia Cruzada, que coloca mais peso nos exemplos difíceis de classificar e reduz a influência dos exemplos fáceis.

$$FL(y, \hat{y}) = - \frac{1}{N} \sum_{i=1}^{N} (1 - \hat{P}_i)^\gamma \cdot CE(y_i, \hat{y}_i)$$

Durante o treinamento, o termo de modulação $(1 - \hat{P}_i)^\gamma$ reduz o impacto das instâncias já bem classificadas (onde a probabilidade prevista $\hat{P}_i$ está próxima do valor correto), permitindo que o modelo dedique mais esforço às instâncias com maior erro.

Há também estudos que defendem o uso de algoritmos de Ensemble para auxiliar em problemas de classes desbalanceadas. Apesar do uso desses modelos não ser, inicialmente, voltado para problemas de classes desbalanceadas e seu uso ser muito mais amplo, a estrutura dos algoritmos de Boosting favorecem naturalmente a eficiência e o funcionamento desses modelos.

Isso ocorre porque modelos desse tipo, como o AdaBoost, têm um objetivo semelhante ao da função de Focal Loss. Esses algoritmos utilizam todo o conjunto de dados para treinar classificadores de forma sequencial, focando nas instâncias mais difíceis de classificar. A ideia é corrigir, a cada iteração, os erros cometidos na iteração anterior.

Dessa forma, eles direcionam maior atenção aos exemplos mais desafiadores, utilizando um sistema de pesos. Inicialmente, todas as instâncias possuem pesos iguais. No entanto, após cada iteração, os pesos das instâncias classificadas incorretamente são aumentados, enquanto os pesos das classificadas corretamente são reduzidos.

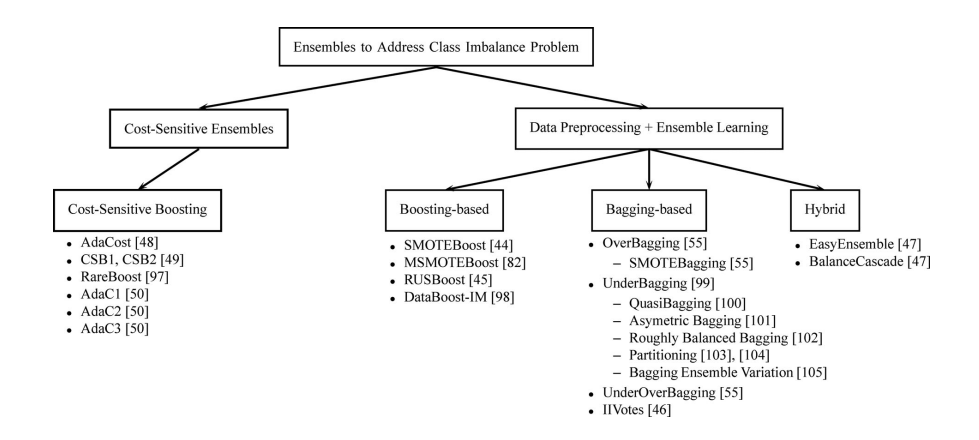
Para quem deseja explorar o tema com mais profundidade, recomendo a leitura do artigo: A Review on Ensembles for the Class Imbalance Problem: Bagging, Boosting, and Hybrid-Based Approaches

Métricas

No nosso exemplo, no início do texto, vimos que menos de 1% das transações são consideradas fraudulentas. Muitas vezes, o desbalanceamento entre as classes é ainda maior, mas vamos considerar essa distribuição para facilitar alguns cálculos.

O uso de métricas incorretamente para avaliar esses modelos pode levar à aceitação de preditores ruins, que não aprenderam a detectar corretamente as classes minoritárias, mas aparentam ser eficientes à primeira vista.

Ao usar a Acurácia (% de predições corretas), por exemplo, como métrica de avaliação, um modelo que simplesmente prevê todas as transações como "não fraudulentas" alcançará uma acurácia de 99%, sem jamais identificar corretamente uma fraude

Isso ocorre porque o cálculo da Acurácia é dominado pela classe majoritária, tornando-a uma métrica insuficiente em casos de desbalanceamento severo.

Além disso, o que queremos não é prever corretamente as transações verdadeiras. Se fosse assim, esse "modelo dummy" seria suficiente. Nosso objetivo é prever corretamente a classe de interesse, no caso, a classe minoritária.

A matriz de confusão (ou matriz de erro) é um método de avaliação de modelos de classificação binária que pode nos ajudar a encontrar métricas mais úteis. Imagine dois modelos, A e B, que foram treinados usando o conjunto de dados mencionado anteriormente e foram usados para fazer predições em dados novos, que nunca foram vistos.

Modelo A	Fraude	Transação
Predição: Fraude	2	8
Predição: Transação	42	948

Modelo B	Fraude	Transação
Predição: Fraude	9	49
Predição: Transação	1	941

Olhando para essas matrizes, qual modelo você escolheria? Ambos os modelos tiveram acurácia de 95%, mas, como vimos, essa não é a métrica mais adequada para avaliar modelos em problemas de classes desbalanceadas. Há outras métricas mais eficientes, como: Precisão, Recall e F1 Score.

A Precisão avalia quantos casos preditos como fraude foram realmente fraudulentos, ou seja, quantas transações realmente foram fraudulentas. Já o Recall, ou Sensibilidade, corresponde à porcentagem de fraudes reais que o modelo conseguiu capturar. Em tarefas de detecção de anomalias, essa é a métrica mais importante.

Isso significa que o modelo está conseguindo identificar a maior parte das fraudes existentes e poucas fraudes estão sendo deixadas de fora. Se muitas fraudes reais não estão sendo detectadas pelo modelo, pode ser problemático em cenários onde a detecção é crucial, como no caso de fraudes de cartões, em que se busca evitar ao máximo os falsos negativos.

Por fim, o F1 Score é a combinação da Precisão e do Recall em um único valor, funcionando como uma métrica que integra ambas para oferecer uma visão mais geral do desempenho do modelo.

Em algumas situações, o objetivo será maximizar o F1 Score; em outras, pode ser mais importante priorizar o Recall, dependendo do contexto e do problema que se busca resolver.

Vamos ver o cálculo dessas métricas para os modelos A e B:

	Acurácia	Precisão	Recall	F1 Score
Modelo A	0.95	0.02	0.1	0.03
Modelo B	0.95	0.15	0.9	0.26

Ao analisar as métricas de avaliação dos modelos, podemos ver que, apesar da acurácia ser a mesma, o Modelo B seria a escolha mais apropriada, devido ao Recall mais alto. Lembrando que essa é uma simulação apenas para exemplificar e nos ajudar a entender o funcionamento dessas métricas.

Para quem quiser entender mais sobre como essas métricas são calculadas, indico o artigo: The Relationship Between Precision-Recall and ROC Curves

Conclusões

A construção de modelos robustos é, inevitavelmente, um processo experimental, que exige ajustes contínuos até alcançar um resultado satisfatório.

Desde a escolha dos algoritmos e métricas de avaliação até a reamostragem ou a adaptação da função de perda, cada abordagem apresenta desafios únicos e benefícios específicos que precisam ser cuidadosamente equilibrados.

Espero ter conseguido transmitir que a escolha das técnicas mais adequadas depende do problema que estamos tentando resolver e das limitações dos nossos dados. Afinal, o objetivo é sempre criar um modelo que não apenas acerte mais, mas que acerte o que realmente importa.

Portanto, da próxima vez que se deparar com um problema de classes desbalanceadas, lembre-se de algumas dessas estratégias e técnicas para auxiliar na robustez do seu modelo.

Referências

[1] C. Huyen, Designing Machine Learning Systems: An Iterative Process for Production-Ready Applications. Sebastopol, CA, USA: O'Reilly Media, 2022.

[2] Nilson Report, "Issue 1187," December 2020. https://nilsonreport.com/newsletters/1187/

[3] M. Galar, A. Fernandez, E. Barrenechea, H. Bustince, and F. Herrera, "A review on ensembles for the class imbalance problem: Bagging, Boosting, and Hybrid-based approaches," IEEE Transactions on Systems, Man, and Cybernetics, Part C (Applications and Reviews), vol. 42, no. 4, pp. 463-484, Jul. 2012. https://doi.org/10.1109/TSMCC.2011.2161285

[4] J. Davis, M. Goadrich. The relationship between Precision-Recall and ROC curves. In Proceedings of the 23rd international conference on Machine learning (ICML '06). Association for Computing Machinery, New York, NY, USA, 233–240, 2006. https://doi.org/10.1145/1143844.1143874

Agradeço a todos que acompanharam até aqui! Nos vemos na próxima :)